Page d'Accueil
- POV-Ray Tutorial
- Géométrie de Base
pour Raytracing
Triangle rectangle
Théorème de Pythagore
Trigonométrie de base
Loi des cosinus
Triangle équilatéral
Polygone régulier
Polyèdre
Tétraèdre régulier
Octaèdre régulier
Cube et Cuboïde
Dodécaèdre régulier
Icosaèdre régulier
Cuboctaèdre
Octaèdre tronqué
Rhombicuboctaèdre
Icosaèdre tronqué
Cercles
Cercles touchants
Tangentes internes
Tangentes externes
- Geometric 3D Animations
|
Note: En POV-Ray nous utilisons "sqrt(X)" pour la racine carrée de X.
Note: Pour eviter chaque collision avec des noms incorporé et des mots réservés de POV-Ray,
il est très recommandé de utiliser seulement des mots que commencent avec des capitals (lettres majuscules)
pour tous les noms des variables declarés par le utilisateur, par ex. on prend "Ri" au lieu de "r"
et "H" au lieu de "h".
|
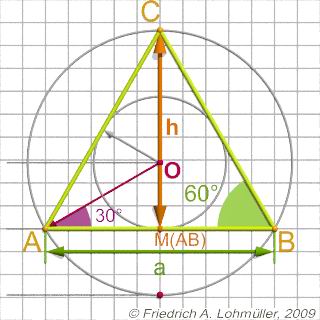
Les Dimensions
Longueur d'un côté de base du triangle: a.
Tous les angles internes: 60° |
L'hauteur
d'un triangle équilatéral:
h = 1/2 * sqrt(3) * a ; or
h = sin (radians(60)) * a ;
L'hauteur du centre O du cercle inscrit, ou
longheur du rayon du cercle inscrit:
r = 1/6 * sqrt(3) * a ;
le rayon du cercle circonscrit
d'un triangle équilatéral:
R = 1/3 * sqrt(3) * a ;
|
|
Un triangle équilatéral
|
|